Mathletics: 1+1=1.5

My daughter’s school recently ran a month-long trial of the “next generation in online Math learning platform” – Mathletics (http://www.mathletics.com).

It’s a site which aims to augment maths teaching/practice for children from 4 to 13. Its ‘next generation’ label comes from the online and gaming aspects which “students love”. I sat down with my daughter to find out how she responded to it.

On logging in, the first thing she did was create an avatar, and choose a character to guide her through the site (so far so good). She then started work on two challenges set by the school: nothing new here – just a series of maths questions with an answer box (just as you might see on paper) – on a right answer, a tick; on a wrong answer, a cross: no feedback or hints on approaches. To complete the challenge, all ten questions have to be answered correctly; any errors, and the whole ten questions (same ones, in order) have to be attempted again.

As a result, she soon got frustrated and gave up on these challenges, then spent a good 30 minutes changing hair, backgrounds, colours etc. on her avatar (the avatar area takes tips from Moshi Monsters et al, and inherits something of the same engagement level). No maths learning here though.

The one redeeming ‘next generation’ feature is a live challenge mode, where you can play against other students from around the world. On starting, you are assigned three other competitors, and a countdown clock starts, as mental maths questions appear on screen: the aim being to answer more than your competitors in the time available. This certainly attracted both of us, but within seconds frustration was back, as all three of the competitors stormed ahead (easily beating our combined efforts): there is no obvious option to filter competitors to different age ranges or skill levels to provide a challenge, rather than an impossible task.

All in all, Mathletics is a poor example of gamification – applying apparently ‘motivating’ aspects of games and playful activities (in this case, the use of customisable avatars and competitive aspects with avatar-rewards) to what is essentially a very traditional try-and-repeat approach to teaching. The gaming aspects add nothing to the experience other than temporarily diverting (and non-learning) activities around the edges.

Puzzles, problems and STEMs

Colin Thomas, Professor of Chemical Engineering at the University of Birmingham, organised an open HEA workshop on the use of puzzles in STEM (Science, Technology, Maths and Engineering) teaching this week. Colin has been using puzzles in his teaching to engage students in some of the core maths skills they need as chemists; and has joined up with colleagues in Mathematics to produce a booklet which collects popular maths puzzles throughout history into a single handy resource.

The workshop, attended by 40 lecturers from across the UK in STEM subjects (and two ‘outsiders’ – myself and a lecturer in Education representing a humanities perspective), was centred around the question of whether maths puzzles could be adapted to other subjects by altering their language and setting. In other words, would adding a relevant context improve students’ engagement with the puzzles and underlying skills?

Firstly, though, we spent the first part of the day trying to solve some of the puzzles Thomas and his colleagues had compiled. This tested my rusty A-level maths skills to their limit, but I managed quite a few to my great satisfaction. It was interesting to note that, although introduced as a solo exercise, very soon all participants were deep in discussion, sharing problems or solutions with each other: puzzle solving can be a highly communal, as well as individual, activity (as I found in my own work with puzzles in History).

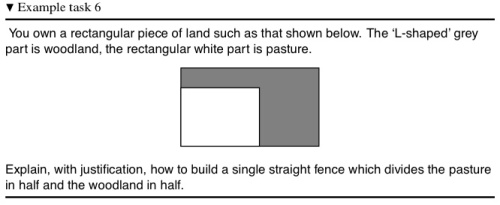
An example puzzle from Badger, Sangwin, Ventura-Medina & Thomas (2012)

Thomas defined ‘puzzles’ as distinct from problem solving and games-based learning (although essentially puzzles can be constituent, though not exclusive, parts of both of these), and drew on the work of Michalewicz and Michalewicz (2008) in their own study of mathematical puzzles, defining educational puzzles with four criteria:

1. having generality (ie. applicability of the principle is wider than the puzzle itself)
2. having simplicity (although I would argue strongly against this: puzzles might be at any level, and most usefully are set just above the current level of the student)
3. having a ‘Eureka’ factor (equivalent to fiero in game design: that moment of pure joy on finding the solution)
4. being entertaining in some way.

There was some discussion of whether puzzles are best used as ‘extra’ activities (outside the curriculum) or embedded within the curriculum itself and linked to assessment and progression. Whilst Thomas had embedded puzzles as additional elements within larger teaching sessions (with greater success than he had found when offering puzzles as an extra option previously), Chris Sangwin described a whole module he had designed in Mathematics, where students were given puzzles to solve in each session, and would then have to present and defend their solution in front of the class. Interestingly, Sangwin found an interesting effect on engagement with the puzzles over the module’s ten-week period: excitement in week 1, frustration in week 3, despondent in week 5, rebuilt confidence in week 7, and confident and collegiate by week 11. Sangwin found that a group size of 10-20 was ideal, and found that some students failed to engage – although with the presentation side rather than the puzzles.

In the afternoon, we worked in small mixed-discipline groups on designing subject contexts around the standard maths puzzles. On my table, this led to some very interesting discussion: would adding subject context overcome the difficulty non-maths students have with mathematics? Whilst some felt that this would simply be superficial and of no benefit, I argued with my own experiences that adding subject context can have a dramatic effect on engagement; but that the context must be carefully thought-out to reflect the character of the subject (so, taking the fields example above, it’s not enough to swap fields for – say – building floor space for Engineering students; students need to feel that they are doing meaningful work towards their future profession – and so the puzzle must reflect a real problem engineers face in their work). The use of narrative though, whilst generally liked within humanities subjects, is – of course – less common/accepted in STEM subjects, and hence many of the participants found this approach quite alien (as, presumably, would their students) and tended to keep returning to the stripped-down source puzzles.

In conclusion, this was a thoroughly interesting workshop, delivering some fascinating discussions which transcended STEM subjects and yet provided an interesting contrast with humanities approaches. As is so often the way, context was agreed to be of great importance, but the character of students and lecturers in particular subjects was brought into the equation. Overarching all of this, however, we all decided that a good puzzle can indeed be highly engaging regardless of your background.